Simulation in Games: Week 2
In this week’s Simulation in Games post, I will go over my understanding of the concepts of displacement and velocity, my implementation of the related exercise and updates on my game ideas!
Vectors, Displacement and Velocity
Vectors (Continued)
- Global/world coordinates - Based on world/scene space. Origin point at (0, 0, 0). The Vector structs contain static properties which act as shorthands for certain global coordinates.
- up (Vector2 and Vector3)
- down (Vector2 and Vector3)
- left (Vector2 and Vector3)
- right (Vector2 and Vector3)
- forward (Vector3 only)
- back (Vector3 only)
- one (Vector2, Vector3 and Vector4)
- zero (Vector2, Vector3 and Vector4)
- positiveInfinty (Vector2, Vector3 and Vector4)
- negativeInfinity (Vector2, Vector3 and Vector4)
- Local coordinates - Based on the object iself; its rotation, parent, etc.
-
Vector visualisation - Vectors can be drawn in Unity’s scene viewport by using the Debug class’s static method DrawRay(). This takes the starting position and direction of the ray, among other, less important parameters.
- Normalized vectors - A normalized vector is the version of a vector where its length becomes equal to 1. This can be achieved by dividing each coordinate of the vector by its magnitude. In Unity, a vector can be normalized using the Normalize method. If the original vector is to remain unchanged, the normalized property can be used to return a normalized copy of the vector.
Displacement
Displacement is the final position of an object relative to its initial position, i.e. moving from one point in space to another. In Unity, objects can be moved by changing their Transform.position properties.
Vector3 finalPosition = new Vector3(5, 6, 3);
directionalVector = finalPosition – startingPosition;
if (Input.GetKeyDown(Keycode.Return) && transform.position != finalPosition)
transform.position = finalPosition;
else if (Input.GetKeyDown(Keycode.Return))
transform.position = startingPosition;
The above code will teleport (displace) the object it is attached to to a final position if the Return key is pressed and it isn’t there yet. Otherwise, it will return it to its starting position.
Velocity
Velocity is the rate of change of an object’s position over time. In Unity, velocity can be represented as a vector with a direction (a normalized vector) and magnitude (speed in the form of a float). The equation for calculating velocity is:
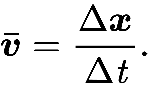
This equation can be rearranged to get an object’s position:
- position = velocity * time
- position = direction * speed * time
This can be used in Unity to smoothly move objects.
Vector3 finalPosition = new Vector3(5, 6, 3);
float speed = 5;
directionalVector = B – A;
transform.position += directionalVector.normalized * speed * Time.deltaTime;
The above example will move the object it is attached to in the direction of the normalized directional vector at a speed of 5 units per second.
Exercise - An Application of Displacement and Velocity
The Tasks
In this week’s practical, we were tasked with creating a Unity project that:
- Contains a cube, Cube A.
- Allows the user to move a second cube, Cube B, with user input. Movement is to be achieved using the concept of directional vectors multiplied by speed. Speed must be a public variable or marked with [SerializeField] to allow the user to modify the speed at will.
- Makes Cube A look at Cube B. This action is to be achieved using directional vectors.
- Makes Cube A follow Cube B if the distance between them is less than N units, where N is a number defined by the user at runtime.
- Makes Cube A chase Cube B after 3 seconds of following it.
The Implementation
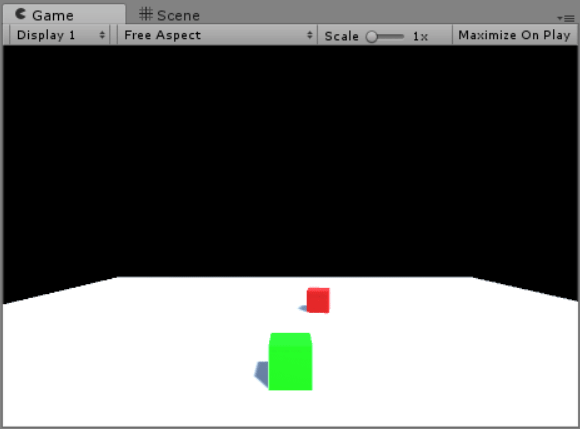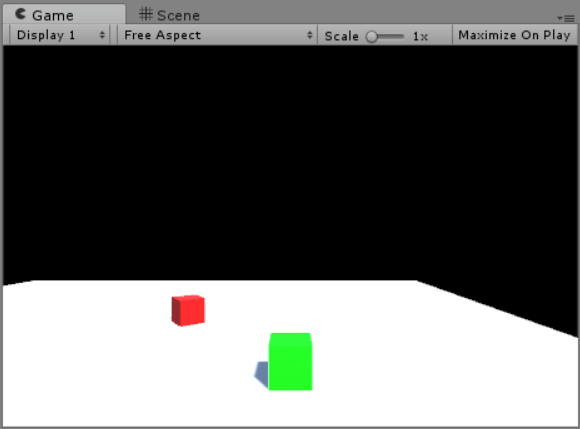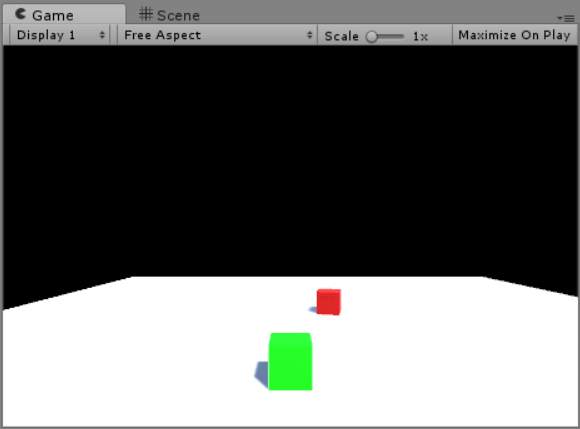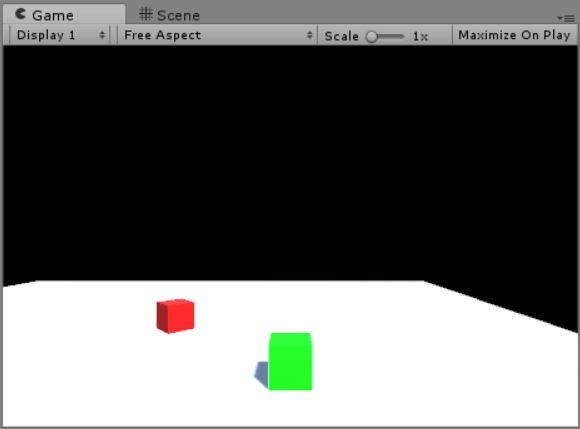
The above GIF demonstrates how Cube A (the red cube) tracks Cube B’s position. This is done by setting transform.forward to the directional vector (Cube B’s position subtracted by Cube A’s).
It also demonstrates Cube B’s movement, which utilizes the velocity equation as described above, tying each of the WASD keys to a different direction.
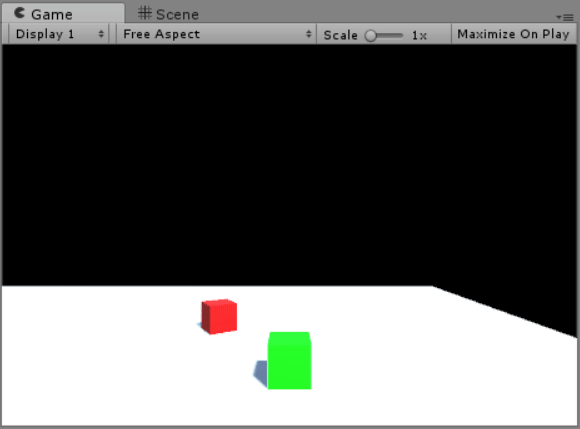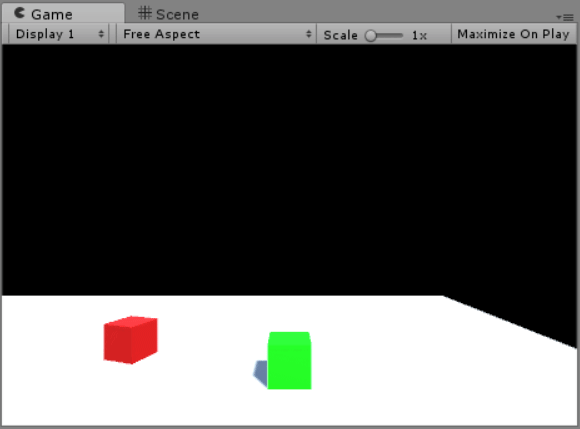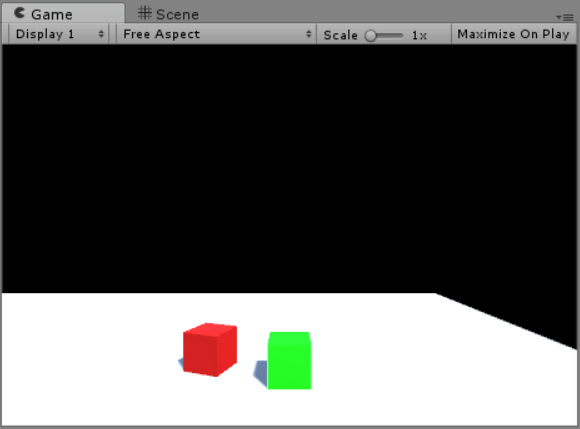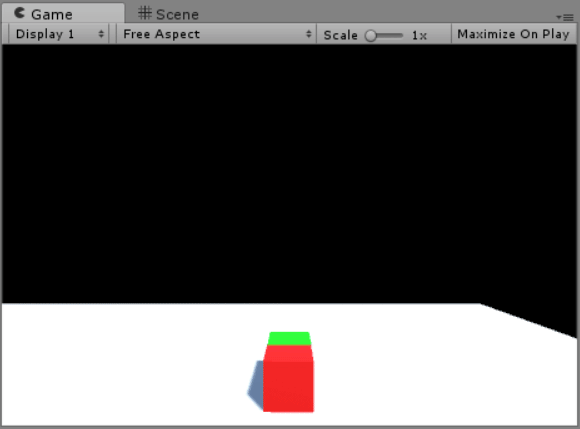
After entering Cube B’s range, Cube A’s position is set to be Cube A’s subtracted by (the normalised directional vector multiplied by N). This ensures that Cube B will always be N units away from Cube A.
3 seconds later, a float variable called follow will reach 0, which will signal Cube B to start chasing Cube A. Its position is now the normalized directional vector multiplied by Cube B’s speed and Time.deltaTime.
Spellcaster Academy
After some more research, I decided to change the title of the project to Spellcaster Academy, as Witchcraft Academy seems to be in use by several “online academies” as well as an online casino slot game.
Anyway, as promised last week, here’s some specifics about the game!
Spellcaster Academy will be a first person game where you take on the role of a wizard with a large arsenal of spells to defeat enemies and solve puzzles. Here are some of the spells I have in mind:
- Shield spell - Protects wizard from enemy attacks. Constant mana drain.
- Healing spell - Converts mana points to health.
- Fireball spell - Standard projectile. Sets things on fire. Low mana cost.
- Freeze spell - Can freeze the enemies and the ground; icy ground has less friction. Low(ish) mana cost.
- Levitation spell - Used to levitate objects. Can be used on unreachable objects or to drop heavy objects on top of enemies. Medium mana cost.
- Black hole spell - Sucks enemies into itself. Large mana cost.
- Explosion spell - Creates an explosion which blows enemies in its vicinity away. Large mana cost.
Thanks for reading. See you next week!
P.S.: I also put together a moodboard. Check it out!